Flare-On 2018 - Challenge 12 - Subleq'n'RSSB
After explaining my solution for the last challenge of Flare-On 2018, I want to
move one and analyze the details of the second stage. I will entirely focus on
two OISC machines: Subleq1 and RSSB2. Take it as a personal training to
tackle these processors and a way to get rid of the curiosity I wasn't able to
eliminate when I firstly scored this challenge.
The goal is to create an IDA Pro processor module to reverse the code fully
statically. This is possible—for humans at least—only if the code can be
translated to an higher level representation. We first analyze the
Subleq and then switch to the RSSB.
Subleq
A Subleq instruction has 3 operands A B C. The memory pointed by A is
subtracted from the memory pointed by B. The result is stored into the memory
address B. If the subtraction result is less than or equal to 0, then the
instruction pointer takes the value of C. If the subtraction result is greater
than 0—or C is 0—the instruction pointer is incremented by 3 to point to
the next instruction.
These conditions are not enough to have readable code. We can divide them in
four new instructions:
CLEAR: ifA == BandC == 0;SUB: ifA != BandC == 0;JMP: ifA == BandC != 0;JLE: ifA != BandC != 0.
With four different instructions it already makes more sense to write an IDA processor.

Look at the IDA graph view result. Not bad at all. We have unconditional and conditional jumps, we recognize an abvious loop and an exit branch. Ah, I manually fixed the addresses of some indirect jumps to get this graph. Graph view would show unlinked branches otherwise.
So far so good. A nice looking picture but still quite unreadable. Reversing
with four instruction for sure is less painful than using only a subleq
instruction. However, we can try to do better and introduce more high level
mnemonics. A great help comes from the official solution of challenge 11 of Flare-On 2017. The author, Nick Harbour, published some macros he wrote and that we can re-implement in IDA.
We start with MOV that he wrote in this way:
.macro MOV(%a, %b) // Move %a to %b
{
MOVJMP(%a, %b, Z)
}
.macro MOVJMP(%a,%b,%c) // Move %a to %b then jump to %c
{
subleq %b, %b
subleq %a, Z
subleq Z, %b
subleq Z, Z, %c
}
The MOV reveals a new pattern.
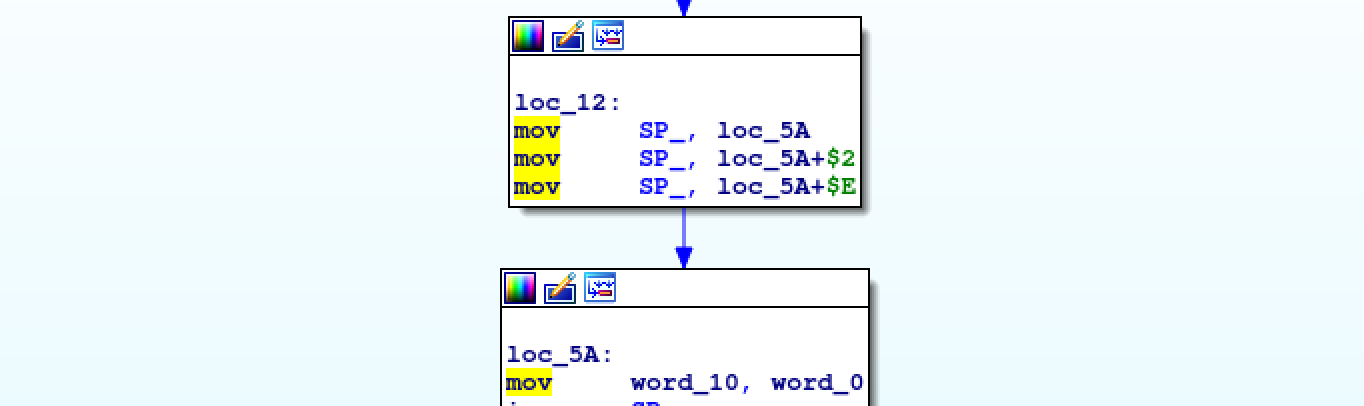
As you can see, there are three MOVs modifying a fourth one. Check what is
modified in the macro above. The three MOVs overwrite the %b operand of the MOVJMP macro.
We call it MOV_DEREF_DST: move A to the memory pointed by deferencing B. The macro is:
.macro MOV_DEREF_DST(%a, %b)
{
MOV(%b, _DEREF_DST)
MOV(%b, _DEREF_DST + 1)
MOV(%b, _DEREF_DST + 7)
_DEREF_DST:
MOV(%a, Z)
}
In a similar way we can write MOV_DEREF_SRC to overwrite the %a operand of the
MOVJMP macro at run-time:
.macro MOV_DEREF_SRC(%a, %b)
{
MOV(%a, _DEREF_SRC + 3)
_DEREF_SRC:
MOV(Z, %b)
}
We can also add some arithmetic instructions like ADD, INC and DEC. The
ADD can be written like this:
.macro ADD(%a, %b)
{
subleq %a, Z
subleq Z, %b
subleq Z, Z
}
%a is negated and stored in register Z and then subtracted from B, thus
giving an addition. INC is an ADD with one:
.macro INC(%a)
{
subleq Z, Z, _ADD
_ONE:
dw 0x1
_ADD:
ADD(_ONE, %a)
}
Last one is DEC:
.macro DEC(%a)
{
subleq Z, Z, _SUB
_ONE:
dw 0x1
_SUB:
subleq _ONE, %a
}
Now our IDA processor has 10 instructions but there is one more sequence we can convert to a macro.
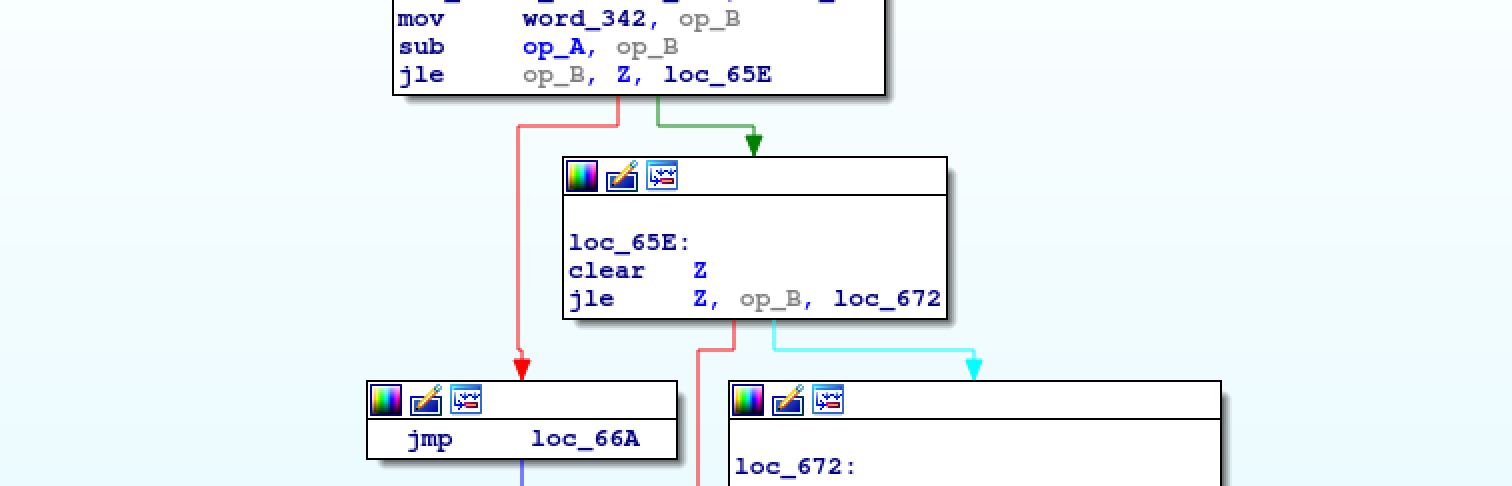
In the picture you can see that A is subtracted from B and the result is
checked to be less than or equal to 0. Immediately after, the
result is checked to be greater than 0. This is a JNE instruction that we
can translate to:

.macro JNE(%a, %b, %c) // Jump to %c if %a != %b
{
MOV(%b, _VAR)
SUB(%a, _VAR)
subleq _VAR, Z, _LESS_EQUAL
subleq Z, Z, _GREATER
_LESS_EQUAL:
subleq Z, Z
subleq Z, _VAR, _EQUAL
_GREATER:
subleq Z, Z, %c
_VAR:
dw 0x0
_EQUAL:
}
The instruction set is quite complete and the new IDA graph view is much much
lighter, beside the fact that the code can be reversed completely statically at this point. Compare the graph on the right with the one at the beginning of the post.
The really cool thing is that we can also see this Subleq code implements
concepts like stack pointer, base pointer for the function frame or function calls. Look at the picture for example.

Once the code is lifted to something more meaningful, the RE pain vanishes. This
Subleq works as interpreter for another inner VM, a Reverse Subtract and Skip if Borrow (RSSB) machine. This also explains why the Subleq traces were incredibly verbose. I release the IDA processor on GitHub implementing all the macros explained so far, so that you can have a closer look at the lifted code. Be aware that I didn't create a macro for indirect jumps—like the one in the POP&RET picture. Either you create it as an exercise, or you extract the value of the POP right before a function return and manually patch the code in IDA. Last thing: this IDA module is an experimental toy highly depending on the macros used in this challenge.
Finally the code of the Subleq captured from IDA and translated to Python.
def dispatch(mem):
ip = mem[0]
if mem[ip] == -1:
return False
mem[1] = (mem[mem[ip]] - mem[1]) & 0xffff
mem[1] = mem[1] - 65536 if mem[1] > 32767 else mem[1]
if mem[ip] != 2:
mem[mem[ip]] = mem[1]
if mem[1] < 0:
return True
return False
mem = [] # RSSB code
size = len(mem)
while mem[0] <= size:
if mem[mem[0]] == -2:
break
if dispatch(mem):
mem[0] += 1
mem[0] += 1
if mem[6] == 1:
mem[6] = 0
chr_out = chr(code[4])
mem[4] = 0
if mem[5] == 1:
mem[5] = 0
mem[3] = ord(chr_in)RSSB
RSSB instructions have one operand A which points to memory. Both Subleq and RSSB
have the IP register mapped to memory location 0x0, but the latter has a second
register mapped at location 0x1: the accumulator ACC. Every rssb instruction
subtracts ACC from A and stores the result in both A and ACC. If the
result is less than 0, the next instruction is skipped. Jumps can be taken by
manipulating the program counter.
RSSB is more extreme than Subleq as you can see. Reversing pure RSSB
instructions would be mind-blowing. We must absolutely recognize some macros,
write an IDA processor module for RSSB and make the code reversable with ease—as we just
did for the Subleq.
The most basic instructions we can implement out of a single rssb are:
CLEAR_ACC: ifA == 1, becauseAwill point toACCthus givingACC-ACC;NOP: ifA == -1, because the RSSB in question jumps to the next instruction without any consideration.
At this point we should stare at our code with three instructions and spot some
patterns which can be converted to an higher-level representation.
The first two are SUB and ADD, with these macros:
.macro SUB(%a, %b) // Subtract %a from %b and store in %b
{
rssb ACC // ACC is at mem 1
rssb %a
rssb 0xffff // NOP
rssb Z // Z is at mem 2
rssb 0xffff
rssb Z
rssb 0xffff
rssb %b
rssb 0xffff
}
.macro SUB_V2(%a, %b) // Subtract %a from %b and store in %b
{
rssb ACC // ACC is at mem 1
rssb %a
rssb Z
rssb Z
rssb Z
rssb %b
}
.macro ADD(%a, %b) // Add %a to %b and store in %b
{
rssb ACC
rssb %a
rssb Z
rssb Z
rssb %b
rssb ACC
}
Let's explain them a bit. In the SUB we reset the accumulator and put %a in
it. Two rssb Z are used to preserve the sign of %a and two NOP to do not
skip instructions depending on the sign. The last instruction will be %b-%a
with %a being in the accumulator. SUB can be written also with three rssb Z without interleaving NOPs, SUB_V2. The effect will be the same.
The ADD is mostly equal except for the missing NOPs. We don't need them
because we want to invert the sign of %a to have %b-(-%a).
Subtraction can also be used to set memory to zero:
.macro CLEAR_MEM(%a) // Set memory at %a to 0
{
SUB(%a, %a)
}
Now let's add unconditional branches with a JMP macro:
.macro JMP(%a) // Jump to %a
{
rssb ACC
ADD(_VAL, IP) // IP is at mem 0
_VAL:
dw (_VAL - %a) // compute jump length
}
You notice how we directly modify the program counter by adding the length of
the jump to it.
What about INC and DEC:
.macro INC(%a) // Increment %a by 1
{
ADD(_ONE, %a)
JMP(_CONTINUE)
_ONE:
dw 0x1
_CONTINUE:
}
.macro DEC(%a) // Decrement %a by 1
{
SUB(_ONE, %a)
JMP(_CONTINUE)
_ONE:
dw 0x1
_CONTINUE:
}
We are still missing MOV and conditional branches, the most important
instructions to understand the control flow of a program. The
challenge author implemented the MOV by using CLEAR_MEM in conjunction with
ADD.

The respective macro is going to be:
.macro MOV(%a, %b) // mov %a to %b
{
CLEAR_MEM(%b)
ADD(%a, %b)
}
After pushing our new macros inside an IDA processor for RSSB, it gets easier to recognize new—more complicated—macros.
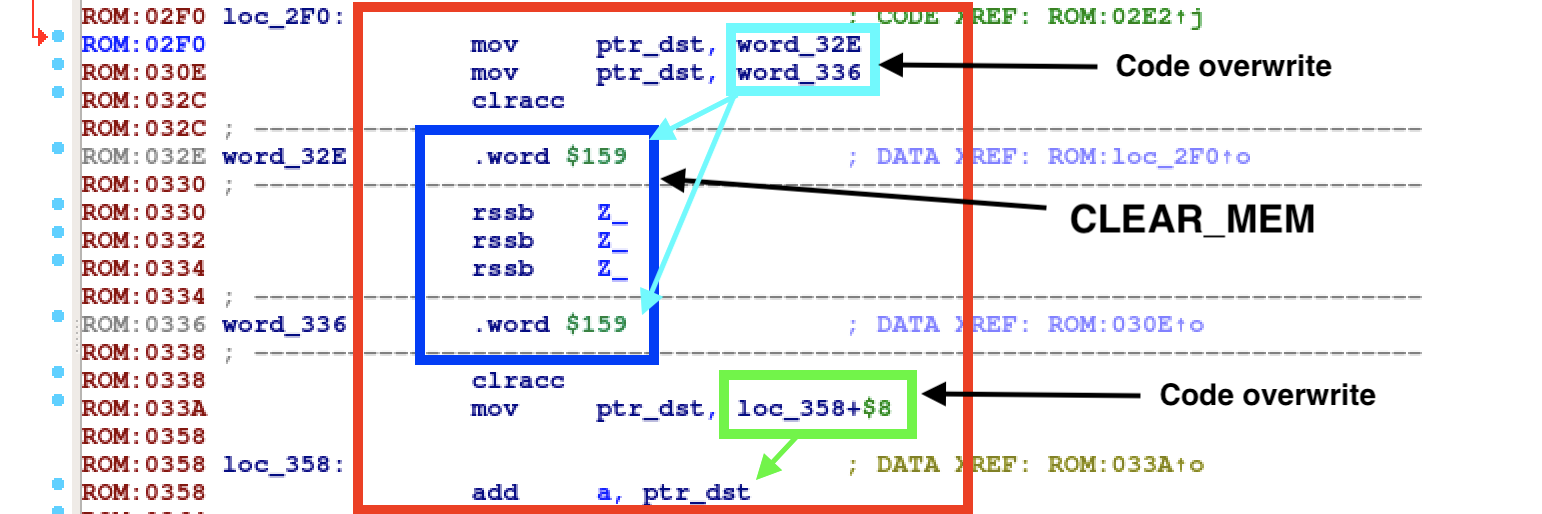
You can see above a MOV_DEREF_DST. Move A to the memory pointed by
dereferencing B. The pretty looking macro will be:
.macro MOV_DEREF_DST(%a, %b) // Move %a to ptr %b
{
MOV(%b, _CLEAR)
MOV(%b, _CLEAR + 4)
rssb ACC
_CLEAR:
SUB_V2(Z, Z)
MOV(%b, _DEREF_DST + 4)
_DEREF_DST:
ADD(%a, Z)
}
MOV_DEREF_SRC is quite similar but a bit shorter.

The macro for MOV_DEREF_SRC is:
.macro MOV_DEREF_SRC(%a, %b) // Move ptr %a to %b
{
CLEAR_MEM(%b)
MOV(%a, _DEREF_SRC + 1)
_DEREF_SRC:
ADD(Z, %b)
}
Conditional branches in our RSSB are more fascinating than all other
instructions. I recognized a JGE / JLE macro by analyzing the last low-level snippet
of code remaining in my IDA disassembly. The RSSB code in IDA is quite long and
would clutter the blog post. Go here to have a look at the big picture.
Try to reason some minutes on the code and maybe you can agree it makes sense to
translate it to a conditional branch. The pattern is not unique tho. Our RSSB
code shows different instructions combinations achieve a JGE behavior. For
example the pattern at offset 0xfd6 of the RSSB memory is slightly different
from the pattern at offset 0x17a4.
Below is what could be a JGE macro. Be aware it doesn't match 1:1 with our
RSSB.
.macro JGE(%a, %b, %c) // Jump to %b if %a >= 0 else %c
{
CLEAR_MEM(_VAR1)
CLEAR_MEM(_VAR2)
rssb ACC
rssb %a
rssb ACC // Skip this if %a < 0
rssb _VAR1 // _VAR 1 is 0 if %a >= 0 else -%a
MOV(_VAR1, _VAR2)}
MOV(_JL, _VAR_JL)
MOV(_JGE, _VAR_JGE)
DEC(_VAR2)
JMP(_L1)
_VAR1:
dw 0x0
_VAR2:
dw 0x0
_VAR_JL:
dw 0x0
_VAR_JGE:
dw 0x0
_VAR3:
dw 0x0
_JL:
dw %c
_JGE:
dw %b
_L1:
rssb ACC
rssb _VAR2
rssb _VAR2 // Here _VAR2 is -1 if %a >= 0 else is 0
INC(_VAR2)
ADD(_VAR2, _VAR3) // Create a jump length of 14
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
ADD(_VAR2, _VAR3)
rssb ACC
rssb _VAR3 // _VAR3 is 0 if %a >= 0 else 14
rssb Z
rssb Z
rssb IP
CLEAR_MEM(_VAR3)
rssb ACC // We get here if %a >= 0
rssb _VAR_JGE
rssb Z
rssb Z
rssb IP
CLEAR_MEM(_VAR3)
rssb ACC // We get here if %a < 0
rssb _VAR_JL
rssb Z
rssb Z
rssb IP
The RSSB IDA processor now counts 14 instructions that allow us to see memory movements, arithmetic operations and control flow decisions. IDA graph view should make a lot of sense by now. And in fact…
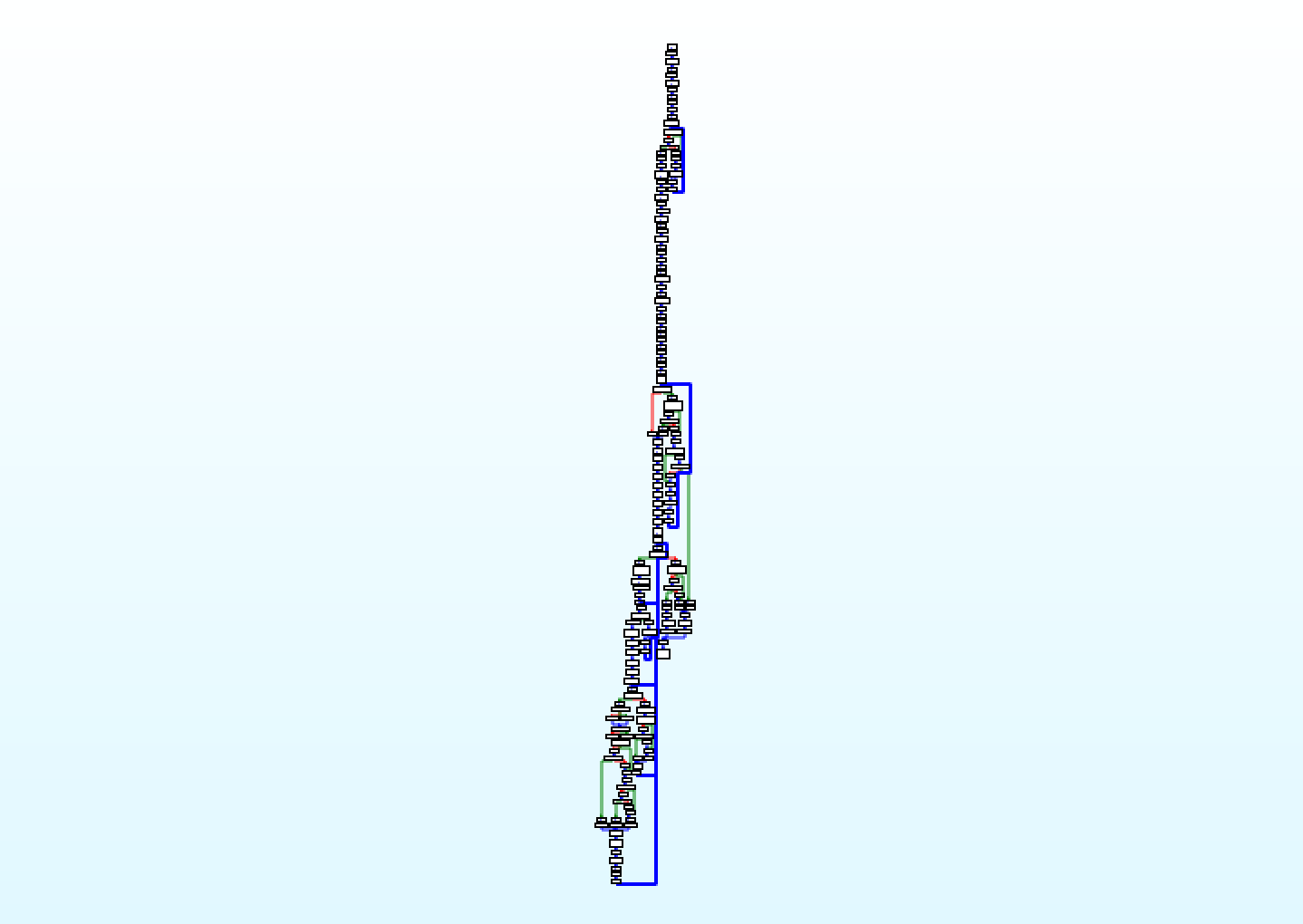
In the first part of this blog post I said my final goal is to reverse the RSSB
statically with IDA Pro. Well, it's possible now. The macros made their job and
reversing the machine doesn't cause a crazy headache anymore. There is also here
the concept of stack, push, pop, base pointer and function call like in the
Subleq. There are indirect jumps as well for which I didn't provide any macro, but
target addresses can be solved by embedding in the IDA module a tiny stack
emulator. The alternative is to patch the code manually as I did.
Actually there is a branch missing in the graph: it goes from the bottom to the small loop you can see in the top part of the image. I didn't
include it on purpose, or IDA would align the basic blocks in a weird way.
Head here for a closer look to the full
graph after lifting the code.
I publish on GitHub also the toy RSSB processor for IDA. What I said for the Subleq module holds for the RSSB one. You can use the IDA processors to experiment, play with it and modify it, but do not expect they will work with other VM code. These processors are NickHarbour-dependent :) and have been coded with no special effort.
Ah, in the cat'n'grep writeup I was wondering what was the big number added to the sum of all input chars up to @ excluded.
Mistery solved—it's (i << 10) + (i << 11), signed and over 16 bits of
course. i is equal to the index of @ in the password.
The python code doing the same encryption as of the RSSB is:
def wrap(val):
return (ord(val[1]) - 32) << 7 | (ord(val[0]) - 32)
def twos_ca(val):
if val >> 15:
return -((1 - val) & 0xffff) + 1
return val
def encrypt(text):
res = []
tot_sum = 0
for i, c in enumerate(text):
c = ord(c)
if c - 0x40 == 0:
tot_sum += (twos_ca(i<<10) + twos_ca(i<<11))
break
else:
tot_sum += c
for i in range(15):
v = wrap(text[i*2:i*2+2])
v = v ^ ((i << 5) | i)
res.append(tot_sum + v)
return resIf you never tried to create an IDA processor module, you can take the following resources as a starting point:
- Hex Rays - Scriptable Processor modules
- Quarkslab - IDA processor module
- IDA SDK
- All the public processors on GitHub
Unfortunately most of the resources you find online are for IDA 6 API. The Subleq and RSSB processors I wrote are for IDA >= 7.